我們來推導一下 Back propagtion 的公式,
首先先設想一個只有兩層的 Neural network 如下:
從上圖我們先列出公式如下:
Z = a * W'
hx = sigmoid( Z )
由前面的經驗我們可以得到,
當我們要對 W 進行更新來最小化分類誤差時, 使用 Gradient descent 來更新 W.
那麼如何求出 W 的 Gradient 呢?
我們可以把這個式子使用連鎖律展開!
第一個跟你的Cost function直接相關的是 output layer (a)
而 a 又是經過 sigmoid (z) 得到的
那 z 就可以跟Wij扯上關係啦!
這樣就可以把式子展開如下:
第一層的微分項, 也就是你的 Cost function 對 prediction value 微分, 可以得到 (y - a)
第二層的微分項, 可以得到 a * (1-a)
第三層的微分項則是可以得到再上一層的output layer a
那麼如果再看到上一層的 Wij 呢?
我們看到回到上述第三層的 partial z 部分, 我們知道它是由前一層的 a * Wij 來的,
所以我們在這邊使用連鎖律再把它展開, 可以得到下面的式子

依此類推就可以得到每一層權重 W 的 gradient 項了~

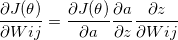


 何...だと...!!
何...だと...!!

